S8. Actividad 1: Integración y redacción del informe final
Investigación documental y de campo
Informe final:
Tema: Estrategias de aprendizaje aplicadas al Álgebra
Nombre
completo:
Fabián
Antonio Condés García
Fecha:
05/Junio/2018
CONTENIDO
ÍNDICE
DE FIGURAS
Introducción
Del artículo de
investigación Larrazolo
N., Backhoff E., & Tirado F.
(2013) las habilidades de razonamiento matemático que adquieren los alumnos del
país
tienen un aprovechamiento sumamente bajo, no comprenden los conceptos básicos
de matemáticas, no tienen las habilidades para solucionar problemas numéricos
de mediana complejidad, y los conocimientos adquiridos se relacionan con la
memorización de algoritmos. Por lo que en mi opinión es indispensable para el mejoramiento de las habilidades de
razonamiento matemático la innovación e implementación de estrategias de
aprendizaje. En este trabajo con base en testimonios de profesores de universidades
e institutos tecnológicos se investigará en el Álgebra, ya que los alumnos preuniversitarios tienen
resultados sumamente bajos en los exámenes de admisión.
En el presente trabajo
se hablará acerca de la metodología de investigación compuesta por tres
apartados: respuesta a una pregunta específica, entrevista y encuesta. También
se hablará acerca de los resultados obtenidos en los siguientes tres apartados:
respuesta a una pregunta específica interpretando la opinión de la Sra. Irma
García, entrevista interpretando la opinión del Sr. Zeth Fabián Villegas y encuesta
por medio de la interpretación en forma de resumen de las 10 preguntas
planteadas a 10 encuestadores mediante gráficas. En el trabajo también se
incluirán recomendaciones y conclusiones a las que se llegaron mediante los
resultados obtenidos de cada apartado. Finalmente se incluirán las fuentes
bibliográficas y de consulta indispensables para recopilar información y
conocer los trabajos de investigación realizados hasta la actualidad.
1. Metodología
Consistió en recopilar información acerca de las
estrategias de aprendizaje del Álgebra mediante respuesta de pregunta
específica, Entrevista y Encuestas dirigidas a alumnos y exalumnos de educación preuniversitaria.
1.1 Antecedentes históricos
1.2 Marco teórico
1.1 Antecedentes históricos
[6] Antúnez,
M., Zarate, J., & Lozano, A. (2014)
realizaron un estudio con 34 alumnos de primer ingreso del nivel medio superior
en una escuela pública. La investigación fué de tipo cualitativa descriptiva,
se analizaron los datos obtenidos de instrumentos como el inventario ILS para
identificar los estilos de aprendizaje, la observación la entrevista, el
cuestionario y el análisis del desempeño. Con la información obtenida se
emplearon estrategias de enseñanza aprendizaje durante un mes y medio y los
resultados indican que los estudiantes se mostraron motivados, con una actitud
positiva hacia las matemáticas y expresaron tener una mejor comprensión.
[7] Santeliz, L.(2006) realizó un aporte teórico,
pues intenta contribuir al desempeño eficiente del docente en la enseñanza del
álgebra, haciendo énfasis en la participación del alumno, fomentando el
desarrollo de habilidades básicas de razonamiento para aprendizajes
significativos, capaz de enfrentarse a tareas exigentes posteriores.
[8] García, M.
(2013) realizó una investigación de corte cualitativo que recuperó los procesos
cognitivos de articulación del aprendizaje de
aritmética al álgebra en alumnos
para identificar e intervenir en aspectos a mejorar de la práctica
educativa.
[9] León, O., Monetti,
J., Schilardi, A., Segura, S. & Rossi, L. (2014) analizaron los valores obtenidos respecto de
los estilos de aprendizaje de alumnos de
primer año de ingeniería, en la Facultad regional de Mendoza de la UTN que
formaron parte de la primera etapa de un proyecto de I+D vinculado al uso de
tecnología de e-learning, para el desarrollo de un sistema adaptativo aplicado
a la enseñanza de Álgebra y Geometría analítica.
[10] Aguiñaga, A., & Mondelo, M. (2016)
realizaron una investigación a nivel teórico acerca de las inteligencias
múltiples y como éstas influyen en el rendimiento académico y el aprendizaje de
los estudiantes en él Álgebra. Al final de éste trabajo se dieron cuenta de que
el alumno muy difícilmente aprende de esta manera, por lo que plantearon el
estudio de la Teoría de las inteligencias múltiples del Dr. Howard Gardner como
una propuesta alternativa de aprendizaje.
[11] Maldonado,
L., Serrano, E., Macías, D., Bernal, R., Rodríguez, G., & Vargas, E. (2009)
presentaron una experiencia sistemática de acompañamiento en el aprendizaje de
las matemáticas con estudiantes de ingeniería, a nivel de pregrado; Los datos
tomados probaron que es una estrategia con resultados muy positivos para los
estudiantes y la actividad pedagógica de los profesores y que puede ser
mejorada a partir del análisis de las redes sociales que se forman, la
introducción de dispositivos de monitoreo y la integración de estrategias de
aprendizaje.
[12] Barros, A.
(2007) realizó un estudio que pretendió explorar las estrategias de aprendizaje
que emplean los estudiantes universitarios en la asignatura de matemáticas uno,
pertenecientes a los programas de ingeniería y tecnología de la Universidad
Tecnológica de Pereira. Como resultado se
encontró que frente a los componentes de las estrategias, prefieren
hacer uso de las técnicas, poseen un metaconocimiento poco reflexivo, tienen
insuficientes conocimientos previos sobre el área, su motivación es extrínseca,
y no hacen regulación y control de sus procesos de aprendizaje.
[13] Águila, M.,
& Allende J.(2012) iniciaron un programa de trabajo conjunto para la
atención a los estudiantes del nivel bachillerato del Centro Escolar
Comunitario del sur de Puebla, México que permitió contribuir al desarrollo de
competencias matemáticas relacionadas con la comprensión lectora. Los
resultados fueron alentadores para docentes y para estudiantes a los que se
sumaron los padres de familia.
[14] Carbonero,
M., & Coromoto, J.(2006) realizaron una investigación centrada en el diseño
y contrastación de un programa de entrenamiento en estrategias de aprendizaje
para las matemáticas en alumnos de educación superior. Los participantes de la
investigación fueron 176 (74 estudiantes que formaron el grupo experimental y
72 que formaron el grupo de control). Los resultados obtenidos permitieron
verificar la eficacia del programa, tanto en el dominio de las estrategias
entrenadas como en las mejoras del rendimiento específico.
[15] Serres, Y.
(2011) analizó que se entiende por álgebra escolar, como se relaciona el
lenguaje y el pensamiento algebraico y la iniciación del aprendizaje del
álgebra, relacionando los procesos de generalización y simbolización con el
desarrollo de las concepciones de variable. Con la resolución de problemas y
con el uso de las calculadoras.
[16] Hernández, A. (2013) realizó una investigación
descriptiva para analizar las estrategias de solución de problemas matemáticos
del Ciclo de Iniciación Universitaria (CIU) de la Universidad Simón Bolívar
sede del Litoral y como el docente apoyó el proceso.
[17] Pifarré,
M. & Sanuy, J. (2001) incluyeron una descripción y justificación de una
secuencia didáctica para mejorar el aprendizaje de las estrategias de
resolución de problemas de estudiantes de educación secundaria.
[18] Inés, S., Del
Valle, M., & Ross, S. (s/año) mostraron los resultados obtenidos al
realizar un diagnóstico para determinar con qué estrategias metacognitivas
contaban los estudiantes de primer año universitario que cursaban Álgebra en el
año 2008.La experiencia arrojó resultados positivos , lo que incentivó a seguir
trabajando en este sentido.
[19] Larrazolo N., Backhoff E., & Tirado F. (2013 investigaron las habilidades de razonamiento matemático que
adquieren los estudiantes mexicanos que egresan del bachillerato y que aspiran
a ingresar a universidades públicas mexicanas. Se analizaron los
resultados de 45 competencias matemáticas del Examen de Habilidades y
Conocimientos Básicos (EXHCOBA), utilizado en los procesos de admisión de 2006
y 2007. Los resultados confirman que los estudiantes: tienen un aprovechamiento
sumamente bajo, no comprenden los
conceptos
básicos de matemáticas, no tienen las habilidades para solucionar problemas numéricos
de mediana complejidad, y los conocimientos adquiridos se relacionan con la
memorización de algoritmos.
Se
concluyó que el sistema educativo mexicano debe esforzarse para mejorar
sustancialmente la educación matemática.
1.2 Marco teórico
Álgebra
Rama de la
Matemática que estudia números, letras y signos. Estudio de propiedades básicas
elementales de números, es la combinación de estructuras abstractas de números
o cantidades, aparece en gran medida la abstracción de conceptos y propiedades
aplicadas a varias situaciones como operaciones aritméticas, operaciones
aplicadas a la vida cotidiana.[1] Meneses, W. ( 2014)
Estrategias para
abordar las dificultades en el algebra
Dentro de las
estrategias de innovación se destacan en el ámbito del álgebra las siguientes:
Estrategias a
partir de las Tecnologías de la Información y las comunicaciones (TIC)
Basadas en la
introducción en el aula de programas y software matemáticos. Los programas más
utilizados en la actualidad para la enseñanza del álgebra se encuadran dentro
de los denominados sistemas de cálculo algebraico, SCA. Los principales y más
utilizados son: “Derive”, “Matlab”, “Mathematica”, “Maple” y “Máxima”. Las
posibilidades simbólicas, numéricas y gráficas que ofrecen este tipo de
programas están provocando numerosos cambios en la enseñanza y aprendizaje de
esta disciplina.
Estrategias usando
los juegos educativos
Para Guzmán
(1984), el juego y la matemática, tienen tantos rasgos comunes que lo hace ser
una estrategia muy importante para transmitir a los alumnos interés y
entusiasmo por aprender matemática. Existen numerosos juegos, en los que se
utilizan herramientas algebraicas como base teórica para su construcción. Con
ellos el estudio del álgebra no sólo se hace más interactivo y de fácil
asimilación, sino, que el juego genera que el aprendizaje sea significativo,
referido a la vida cotidiana. Entre juegos algebraicos a emplear en el aula
destacan, juegos de adivinar números, juegos con tarjetas, dominós algebraicos,
pasatiempos algebraicos, el cuadrado mágico algebraico, la rueda algebraica,
etc. [2] Solano, C. (2013).
Aprendizaje
El aprendizaje
humano está relacionado con la educación y el desarrollo personal. Debe estar
orientado adecuadamente y es favorecido cuando el individuo está motivado. El
estudio acerca de como aprender interesa a la neuropsicología, la psicología
educacional y la pedagogía. El aprendizaje es el proceso mediante el cual se
adquiere una determinada habilidad, se asimila una información o se adopta una
nueva estrategia de conocimiento y acción. El aprendizaje es un proceso por
medio del cual la persona se apropia del conocimiento, en sus distintas
dimensiones: conceptos, procedimientos, actitudes y valores.
Estrategias
didácticas
El término método,
éste se utiliza con frecuencia referido a determinado orden sistemático
establecido para ejecutar alguna acción o para conducir una operación y se
supone que para hacerlo ha sido necesario un trabajo de razonamiento.
El concepto de
método también ha sido muy utilizado en el ámbito pedagógico con ese mismo
nombre, o bien con el nombre equivalente de estrategia didáctica (Gimeno,
1986). Sin embargo, el concepto de método en un sentido estricto debería
reservarse a los procedimientos que obedecen a algún criterio o principio
ordenador de un curso de acciones. En cuanto al orden que se debe seguir en un
proceso, es preferible utilizar el término método cuando se hace referencia a
pautas, orientaciones, guías de la investigación o de la adquisición de
conocimientos que estén bien definidos. La estrategia es una guía de acción que
da sentido, coordinación y orientación a todas las acciones para obtener los
resultados y llegar a la meta, por lo tanto, la estrategia debe estar fundamentada
en un método. La estrategia a diferencia de un método es flexible y puede tomar
forma con base a las metas.
La estrategia
didáctica, responde en un sentido estricto, a un procedimiento organizado,
formalizado y orientado para la obtención de una meta claramente establecida.
Al entender que la
estrategia didáctica es el conjunto de procedimientos, apoyados en técnicas de
enseñanza, que tienen por objeto llevar a buen término la acción pedagógica del
docente, se necesita orientar el concepto de técnica como procedimientos
didácticos y el recurso particular para llevar a efecto los propósitos
planeados desde la estrategia.
Álgebra (del árabe
“al jebr”) es la rama de la matemática que estudia la cantidad considerada del
modo más general posible. Puede definirse como la generalización y extensión de
la aritmética.
El álgebra
clásica, que se ocupa de resolver ecuaciones, utiliza símbolos en vez de
números específicos y operaciones aritméticas para determinar como usar dichos
símbolos. El Álgebra moderna ha evolucionado desde el álgebra clásica al poner
más atención en las estructuras matemáticas. El Álgebra elemental es la forma
más básica del álgebra . A diferencia de la aritmética en donde solo se usan
los números y sus operaciones aritméticas (como +,-,x,/), en álgebra los
números son representados por símbolos (usualmente a, b, c, x, y, z).
Esto es útil porque:
·
Permite la formulación general de leyes de
aritmética (como a + b = b + a) y esto es el primer paso para una exploración
sistemática de las propiedades de los números reales.
·
Permite referirse a números “desconocidos”,
formular ecuaciones y el estudio de cómo resolverlas.
·
Permite la formulación de relaciones
funcionales. [3] Palacio, R. (2013).
ABP
El ABP es una
metodología centrada en el aprendizaje, en la investigación y reflexión que
siguen los estudiantes para llegar a una solución ante un problema planteado
por el profesor.
Técnica de
aprendizaje
Técnicas: acciones
específicas que llevan a cabo los estudiantes cuando aprenden, como puede ser:
repetición, subrayar, esquemas, realizar preguntas, deducir, inducir, etc.
Pueden ser
utilizados de forma mecánica
Estrategia: Se
considera una guía de las acciones que hay que seguir. Son dirigidas a un
objetivo relacionado con el aprendizaje. [5]
Ing. Martínez, H. (2014).
1.3 Respuesta a una pregunta específica
Consistió en recopilar
información acerca de ¿Cuáles eran las estrategias de enseñanza utilizadas en el Álgebra por sus profesores cuando eran estudiantes? , frente a frente,
preguntado abiertamente, haciéndose una plática de emisor receptor sobre la
experiencia que habían tenido para
conocer su opinión acerca del tema y
plantear una breve hipótesis que describa el problema planteado.
1.4 Entrevista
Consistió en elaborar una guía
de preguntas abiertas con un límite de 10 preguntas y aplicar una entrevista
dirigida a un alumno, exalumno o un profesor experto en el tema. Para efectos
de este proyecto de investigación se realizó una entrevista compuesta por 6
preguntas para recopilar información del tema acerca de la dificultad de
aprender temas del Álgebra, facilidad de aprender temas del álgebra,
implementación del profesor de Álgebra de estrategias de aprendizaje a partir
de juegos didácticos, de las TIC´s,
Recomendación de estrategias de aprendizaje a implementar, y Estrategias
de aprendizaje utilizadas para el dominio de temas del Álgebra. En la figura
1.1 se muestra el formato de Guía de preguntas planteadas para aplicar la
Entrevista.
1.5 Encuesta
Consistió en elaborar un
formato de guía de 10 preguntas de tipo opción múltiple y casillas de verificación, es decir la opción
múltiple representa seleccionar una sola opción y las casillas de verificación
equivale a seleccionar más de una opción. El formato de la encuesta fué
elaborado en Microsoft Word y para su aplicación a alumnos, exalumnos de
educación preuniversitaria se realizó mediante los formularios de Google,
haciendo la aplicación de las encuestas más dinámica, y rápida como se muestra
en la figura 1.2.
Figura 1.2 Encuesta compuesta de
10 preguntas aplicada mediante los formularios de Google a 10 alumnos,
exalumnos preuniversitarios
El objetivo de la encuesta fué
recopilar información acerca de la diferencia entre el Álgebra y la aritmética,
Importancia del Álgebra en la solución de problemas de la vida cotidiana,
Importancia de la Aritmética en la solución de problemas de la vida cotidiana,
Conocimiento de temas de Álgebra, Conocimiento de programas para la enseñanza
del Álgebra, Conocimiento de Juegos de Álgebra, conocimiento de métodos de
solución de sistemas de ecuaciones y conocimientos en la solución de problemas
de sistemas de ecuaciones.
1.6 Programa de trabajo
Consiste en distribuir actividades y recursos para cumplir
con el objetivo general y objetivos específicos del proyecto de investigación durante un determinado tiempo (semanas).
Semanas (periodos tentativos)
|
Descripción
|
Recursos
|
|||
Actividad
|
1
|
2
|
3
|
||
Investigación
teórica
|
Lunes
14 de Mayo al Domingo 27 de Mayo del 2018
|
·
Investigar estrategias de aprendizaje utilizados en el
algebra, ejemplos donde se apliquen las estrategias de aprendizaje en el
Álgebra.
|
·
Revistas
·
Artículos
·
Libros
·
YouTube
|
||
Diseño,
creación, ejecución y resultados de la encuesta
|
Lunes 28 de Mayo al Domingo 3 de Junio del
2018
|
·
Investigar tipos de encuestas, proceso para elaborar una
encuesta
·
Diseñar, crear y aplicar una encuesta que permita conocer
las estrategias de aprendizaje aplicados al algebra por estudiantes preuniversitarios
de Toluca, Estado de México.
·
Obtener los resultados de la encuesta mediante gráficas
estadísticas que representen las estrategias de aprendizaje más usadas por
estudiantes preuniversitarios de Toluca, Estado de México
|
·
Microsoft Word 2016
·
YouTube
|
||
Elaboración
y publicación de un video audiovisual
|
Lunes 4 de Junio al Domingo 10 de Junio del
2018
|
·
Investigar como elaborar presentaciones en PowerPoint.
·
Elaborar un video audiovisual que permita comunicar los
resultados obtenidos de la encuesta y aportar recomendaciones para mejorar las estrategias de aprendizaje
aplicadas al Algebra.
·
Publicar el video audiovisual en redes sociales para informar los
resultados obtenidos.
|
·
PowerPoint 2016
·
YouTube
|
||
2. Resultados
2.1 Respuesta a una
pregunta específica
Preguntándole a la Sra. Irma
García ¿Cuáles fueron las estrategias de enseñanza utilizadas por su profesor
de Álgebra? nos respondió que sus Maestros habían sido muy buenos, es decir
tenían un nivel alto de conocimientos, El Maestro explicaba el tema, resolvía
dudas ,enseñaba a resolver ejercicios demostrativos y finalmente el Maestro los
ponía a practicar con ejercicios de tarea, además cuando había exámenes hacían
formularios y hacían Guías de estudio.
2.2 Entrevista
La entrevista se le realizó al
Sr. Zeth Fabián Villegas ex alumno de la prepa en línea SEP, actualmente
estudiando la licenciatura en Administración; Nos comentó que entre los temas
más difíciles del Álgebra esta el convertir del lenguaje natural al lenguaje
algebraico ya que se requiere de un buen nivel de interpretación para dominar el tema; también entre los temas
más fáciles de aprender en el Álgebra son los signos de agrupación ya que para
resolverlos se utiliza la jerarquía de operaciones y operaciones aritméticas.
También estuvo de acuerdo en implementar estrategias de aprendizaje a partir de
juegos didácticos ya que haría el aprendizaje más significativo y más fácil
para dominar temas del Álgebra. Estuvo de acuerdo en la implementación de
estrategias de aprendizaje a partir de las TIC´s, pero sólo cuando se trata de
comprobación, ya que por el lado contrario se obstruiría su proceso de
aprendizaje; Recomendó la implementación de medios audiovisuales como
videojuegos, películas y videos educativos para la mejora de las estrategias de
aprendizaje del Álgebra y finalmente cuando se le preguntó Cuál estrategia de
aprendizaje utilizaría para dominar algún tema de Álgebra si su profesor le
pidiera que lo expusiera, él nos respondió que la lectura, para sintetizar los
puntos relevantes .
2.3 Encuesta
la Encuesta realizada a 10
alumnos, exalumnos preuniversitarios se realizó de forma anónima ya que resultó
por propia experiencia convencer a los participantes a responder la encuesta
difícil. Los resultados de la encuesta se pueden presentar en forma de resumen
y de forma individual, para este caso solo se presentarán en forma de resumen.
En general el 60% de los encuestados sabía la diferencia entre el Álgebra y la
aritmética, mientras que el 40% no respondió acertadamente; el 80% de los
encuestados considera el álgebra como un área de la matemática importante para
la solución de problemas de su vida cotidiana mientras que el 20% no piensa lo
mismo; En el caso de la Aritmética los encuestados están más convencidos con un
90% que es importante para la solución de problemas de su vida cotidiana,
mientras que tan sólo el 10% piensa lo contrario; Consideran el 60% de los
encuestados que la aritmética es el área de la Matemática más indispensable
para la solución de problemas de su vida cotidiana entre el Álgebra y la
Aritmética, mientras que un 40% piensa lo contrario; Para la pregunta cuál de
los siguientes temas de Álgebra conoces el 80% de los encuestados conocían las
ecuaciones enteras de primer grado y ecuaciones de segundo grado con una
incógnita, el 70% conocía el máximo común divisor, el 60% conocía la
descomposición factorial y sólo el 20% no conocía ninguno de los temas como se
muestra en la figura 2.1
Para la pregunta 6 el 50% de
los encuestados no conocían ningún programa matemático, el 30% conocían Matlab,
el 10% conocía Mathematica y Derive, mientras que ninguno de los encuestados
conocía Maple y Máxima como se muestra en la figura 2.2
Figura
2.2 Resultados de la
pregunta 6 ¿Cuál de los siguientes programas para la enseñanza del Álgebra
conoces?
Para la pregunta 7 el 70% de
los encuestados conocía el dominó algebraico, el 50% el juego de adivinar
números, el 40% el cuadrado mágico, el 10% conocía el juego pasatiempos, el 10%
no conocía ninguno de los anteriores y nadie conocía el juego de rueda.
En la pregunta 8 el 90% de los
encuestados conocía el método de igualación, el 60% conocían el método de
sustracción y sustitución, el 50% conocía el método de determinantes y el
gráfico y el 10% no conocía ninguno de los anteriores. Para la pregunta 9 que
consistió en plantear las ecuaciones lineales del problema el 90% planteó
correctamente las ecuaciones y el 10% no sabían como convertir un problema de
lenguaje natural a lenguaje algebraico.
Finalmente en la pregunta 10
que consistió en encontrar el precio de cada prenda, el 70% contestó acertadamente,
mientras que el 30% no llegó al resultado correcto.
3. Conclusiones y recomendaciones
·
los resultados obtenidos del apartado respuesta
a una pregunta específica se concluye que la forma de enseñanza del Álgebra por
profesores no ha tenido innovación en los últimos años ya que hasta la
actualidad se siguen utilizando las mismas estrategias de enseñanza del Álgebra
por profesores y en consecuencia no ha habido innovación en las estrategias de
aprendizaje del Álgebra por los alumnos.
·
Los resultados obtenidos del apartado
entrevista y encuestas se concluye que
la implementación de estrategias de aprendizaje a partir de las TIC´s, es decir
programas o software de matemáticas y estrategias de aprendizaje a partir de
juegos didácticos mejoraría las estrategias de aprendizaje del Álgebra.
·
Los resultados obtenidos del apartado
entrevista se concluye que debe buscarse un aprendizaje más significativo
mediante la implementación de videojuegos, videos educativos, películas y menos
repetitivo y frustrante o tedioso para los alumnos preuniversitarios.
·
Se recomienda innovar e implementar estrategias de enseñanza y aprendizaje del
Álgebra para obtener mejores resultados en el proceso de enseñanza-aprendizaje
del Álgebra.
4. Referencias y fuentes de consulta
4.1 Tesis
[1] Meneses, W.
(2014). Las estrategias didácticas
utilizadas para la enseñanza aprendizaje de álgebra, en el primer año común del
bachillerato general unificado del colegio universitario UTN, en el año lectivo
2013 – 2014 (Tesis de grado). Universidad técnica del norte, Ibarra.
[2] Solano, C. (2013). Los juegos educativos
como mejora en la enseñanza y aprendizaje del álgebra en 3° E.S.O (Trabajo fin
de máster), Cartagena, Murcia.
[3] Palacio, R. (2013). Estrategias
metodológicas aplicadas en el aprendizaje del álgebra en los estudiantes del
octavo grado del colegio Ángela Moreira medina periodo 2010 a 2013
(Monografía), Nicaragua.
[4] Fernández, F. (2013). Estrategias didácticas
para fortalecer el aprendizaje de la matemática en la transición de la
aritmética al álgebra (Tesis de grado). Universidad católica de Manizales,
Manizales.
[5] Ing. Martínez, H. (2014). La aplicación del aprendizaje basado en problemas (ABP) como
estrategia para potenciar el aprendizaje académico en el módulo de algebra con
los estudiantes de primer semestre de la facultad de ingeniería en sistemas
electrónica e industrial de la universidad técnica de Ambato (Trabajo de titulación grado académico de
Magister ), Ambato, Ecuador.
4.2 Artículos
científicos
[6] Antúnez,
M., Zarate, J., & Lozano, A. (2014).
El
aprendizaje de las matemáticas a través de la consideración de los estilos de
aprendizaje en alumnos del nivel medio superior. Revista de Investigación Educativa de la
Escuela de Graduados en Educación, 5(9), 14-20.
[7] Santeliz,
L.(2006). Fundamentos
didácticos en el proceso de
enseñanza-aprendizaje del algebra,
educare, 10(2), 1-12.
[8]
García, M. (2013). Los procesos cognitivos en el aprendizaje del álgebra, Actas
del VII CIBEM, 1233-1240.
[9] León,
O., Monetti, J., Schilardi, A., Segura, S. & Rossi, L. (2014). Estilos de aprendizaje y enseñanza de la
matemática en ingeniería, Congreso Iberoamericano de Ciencia,
Tecnología, Innovación y Educación, 1-8.
[10] Aguiñaga, A., & Mondelo, M. (2016). Empleo de inteligencias múltiples para
mejorar el aprendizaje del álgebra, Revista De divulgación científica jóvenes
de ciencia, 2(1), 994-998.
[11] Maldonado,
L., Serrano, E., Macías, D., Bernal, R., Rodríguez, G., & Vargas, E.
(2009). El Acompañamiento Como Estrategia Pedagógica
En El Aprendizaje Exitoso De Las Matemáticas, Entre ciencia e ingeniería, 3(6),
33-59.
[12] Barros, A.
(2007). Estrategias de aprendizaje empleadas por
los estudiantes para resolver problemas matemáticos, Scientia Et Technica,
13(34), 477-482.
[13] Águila, M.,
& Allende J.(2012). La lectura como estrategia de aprendizaje de
las matemáticas, Congreso Iberoamericano de las Lenguas en la
Educación y en la Cultura / IV Congreso Leer.es, 1-13.
[14] Carbonero,
M., & Coromoto, J.(2006). Entrenamiento de
alumnos de Educación Superior en estrategias de aprendizaje en matemáticas, Psicothema,
18(3), 348-352.
[15] Serres, Y.
(2011). Iniciación del aprendizaje del álgebra y
sus consecuencias para la enseñanza, Sapiens. Revista Universitaria de
Investigación, 12(1), 122-142.
[16] Hernández, A. (2013). Estrategias
de solución de problemas matemáticos en estudiantes Preuniversitarios, I
CEMACYC, 1-9.
[17] Pifarré, M. &
Sanuy, J. (2001). La enseñanza de estrategias de resolución de problemas matemáticos
en la eso: un ejemplo concreto, Enseñanza de las ciencias, 19(2), 297-308.
[18]
Inés, S., Del Valle, M., & Ross, S. (s/año). Estrategias metacognitivas en el aprendizaje del álgebra, Comité
Latinoamericano de Matemática Educativa A. C., 459-467.
[19] Larrazolo N., Backhoff E., & Tirado F. (2013). Habilidades de
razonamiento matemático de estudiantes de educación media superior en México,
18(59), 1137-1163.
5. Anexos
5.1 Guión de entrevista
Inicio de la entrevista no
estructurada
Se dio la bienvenida, luego se
explicó que el objetivo de la entrevista era conocer su opinión en cuánto a las
estrategias utilizadas para el aprendizaje del Álgebra. Se agradeció el haber
aceptado la entrevista, y se pidió permiso para grabar/transcribir la
entrevista. El estudiante accedió a ser grabada/transcrita la entrevista. La
hora de inicio de la entrevista fue a las 5:30 p.m.
1.- En tu opinión, ¿Cuáles son
los temas del Álgebra que son más difíciles de aprender? ¿ por qué?
(Ejemplo: Ecuaciones simultáneas de primer grado con dos incógnitas,
Ecuaciones simultáneas de primer grado con tres o más incógnitas, estudio del
trinomio de segundo grado)
2.- En tu opinión,
¿Cuáles son los temas del Álgebra que son más fáciles de
aprender? ¿por qué? (Ejemplo: Regla de tres, Signos de agrupación,
Descomposición factorial, Ecuaciones enteras de primer grado con una incógnita)
3.- ¿Te gustaría que tu
profesor de Álgebra implementará estrategias a partir de juegos educativos para
mejorar su aprendizaje? (Ejemplo: juegos de adivinar números, juegos con
tarjetas, dominós algebraicos, pasatiempos algebraicos, el cuadrado mágico
algebraico, la rueda algebraica)¿Por qué?
4.- ¿Te gustaría que tu profesor de
Álgebra implementará estrategias a partir de las TIC para mejorar su
aprendizaje?, es decir la introducción en el aula de programas y software
matemáticos. (Ejemplo: “Derive”, “Matlab”, “Mathematica”, “Maple” y
“Máxima”) ¿Por qué?
5.- ¿Cuáles otras estrategias de
aprendizaje recomendarías a tu profesor de Álgebra que fueran implementadas?
(Ejemplo: Videos con las aplicaciones del Álgebra a la vida cotidiana,
Películas) ¿Por qué?
6.- Si tu profesor de
Álgebra te pidiera que expusieras algún tema
¿Cuál estrategia de aprendizaje utilizarías para dominar
el tema?( Ejemplo: Leer, subrayar, y resumir.)
5.2 Encuesta
Objetivo.
Recopilar información acerca de las estrategias de aprendizaje del Álgebra.
1.
¿Cuál crees que sea la diferencia entre el
Álgebra y la Aritmética?
A)
En Aritmética las cantidades se representan por
números que expresan valores determinados y en el Álgebra las cantidades se
representan por medio de letras que pueden representar todos los valores
B)
En
Aritmética las cantidades se representan por medio de letras que pueden
representar todos los valores y en el Álgebra las cantidades se representan por
números que expresan valores determinados
C)
Todas las anteriores
D)
Ninguna de las anteriores
2.
¿Consideras el Álgebra como un área de la
Matemática importante para la solución de problemas en tu vida cotidiana?
A)
Si
B)
No
3.
¿Consideras la Aritmética como un área de la
Matemática importante para la solución de problemas en tu vida cotidiana?
A) Si
B) No
4.
En tu opinión ¿ Cuál área de la Matemática es
más indispensable para la solución de problemas en tu vida cotidiana?
A) Aritmética
B) Álgebra
5.
¿Cuál de los siguientes temas de Álgebra
conoces?
A) Descomposición factorial
B) Ecuaciones enteras de primer grado con una
incógnita
C) Máximo común divisor
D) Ecuaciones de segundo grado con una incógnita
E)
Ninguno de los anteriores
6.
¿ Cuál de los siguientes programas para la
enseñanza del Álgebra conoces?
A)
Derive
B)
Matlab
C)
Mathematica
D)
Maple
E)
Máxima
F)
Ninguno de las anteriores
7.
¿ Cuál de los siguientes juegos algebraicos
conoces ?
A) Adivinar
números
B) Dominós
C) Pasatiempos
D) Cuadrado
mágico
E) Rueda
F) Ninguno
de los anteriores
8.
¿Cuál de los siguientes Métodos de solución de Sistemas de ecuaciones conoces?
A) Método de Sustracción
B) Método de Igualación
C) Método de Sustitución
D) Método de determinantes
E) Método Gráfico
F) Ninguno de los anteriores
Problema. El costo total de la
primera compra de 6 camisetas de mujer y 5 pantalones para hombre es de $
215.00; el costo total de la segunda compra de otras 3 camisetas de mujer y 4
pantalones de hombre es de $145.00.
9.
Con base en el Problema, ¿Cuáles son las
ecuaciones lineales que plantearía usted para obtener el sistema?
A)
B)
C)
D)
10. Con
base en el problema de la pregunta anterior,¿ Cuál fué el precio de cada
camiseta de mujer y el precio de cada pantalón de hombre. Recuerde que el
precio de cada prenda debe satisfacer las ecuaciones lineales planteadas.(
Considere x= precio de cada
camiseta de mujer y y=precio de cada
pantalón de hombre).
A)
B)
C)
D)








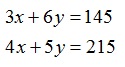






Comentarios
Publicar un comentario